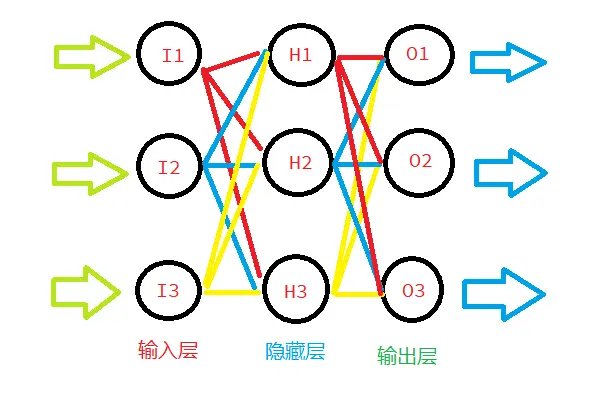
一个简单的神经网络模型

前几天看了本《Python神经网络编程》的书，把一个最简单的神经网络MNIST手写数字识别讲的挺详细的（至少我这个完全的门外汉看懂了）。写个博客展示一下成果。为了SEO，再多写几句。这个神经网络模型基于 numpy 实现，有一个隐藏层，准确率达到95%。

简单介绍

这是一个基于python的最简单的神经网络模型，使用了numpy库，使用的是输入层 - 隐藏层 - 输出层的结构，每一层的节点数自可定义。原理图：

激活函数是经典的：

$$f(x)=\frac{1}{1+e^{-x}}$$

误差函数的斜率：

$$\frac{dE}{dW_{j,k}}=-(t_k-o_k)\cdot sigmoid(\sum_{j}w_{j,k}\cdot o_j)\cdot \\(1-sigmoid(\sum_jw_{j,k}\cdot o_j))\cdot o_j$$

使用矩阵简化运算：

$$\Delta W_{j,k}=\alpha\cdot E_k\cdot O_k(1-O_k)\cdot O^T_j$$

代码很短、很简单，但效果却还不错。

输入层、隐藏层、输出层节点数分别784、100、10个，经过 MNIST手写数字数据集 的训练后，跑了10000个测试，手写数字识别准确率达到了95%左右。

代码

neuronframe.py

import numpy


def activate(x):
    return 1 / (1 + numpy.exp(-x))


class NeuralNetwork:
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate=0.3):
        # set number of nodes in each input, hidden, output layer
        # 分别是：输入层、隐藏层、输出层的节点数
        self.inodes = inputnodes
        self.hnodes = hiddennodes
        self.onodes = outputnodes

        # learning rate
        # 学习速率
        self.lr = learningrate

        # weights
        # 使用正态分布初始化权重
        self.wih = numpy.random.normal(0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
        self.who = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.onodes, self.hnodes))

    def query(self, inputs_list):
        # 计算每个数字的概率

        # 翻转矩阵
        inputs = numpy.array(inputs_list, ndmin=2).T
		# 输入进隐藏层的数据与权重相乘
        hidden_inputs = numpy.dot(self.wih, inputs)
        # 激活函数
        hidden_outputs = activate(hidden_inputs)
		# 输入进输出层的数据与权重相乘
        final_inputs = numpy.dot(self.who, hidden_outputs)
        # 激活函数
        final_outputs = activate(final_inputs)

        return final_outputs

    def train(self, inputs_list, targets_list):
        # 误差计算函数
        inputs = numpy.array(inputs_list, ndmin=2).T
        targets = numpy.array(targets_list, ndmin=2).T

        hidden_inputs = numpy.dot(self.wih, inputs)
        hidden_outputs = activate(hidden_inputs)

        final_inputs = numpy.dot(self.who, hidden_outputs)
        final_outputs = activate(final_inputs)

        # errors
        # 误差值
        output_errors = targets - final_outputs
        hidden_errors = numpy.dot(self.who.T, output_errors)

        # update the weights for the links between the hidden and output layer
        # 根据误差调整权重
        self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs))
        # update the weights for the links between the hidden and output layer
        # 根据误差调整权重
        self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs))