跳到主要内容

特征根法求二阶线性递推数列通项

· 阅读需 4 分钟
Skyone
Skyone
科技爱好者

在上一篇文章中提到过数列二阶线性递推的特征根法，这篇文章来详细介绍一下。

先放出斐波那契数列的通项看看：

xn=15[(1+52)2−1−52)2]x_n=\frac{1}{\sqrt5}[(\frac{1+\sqrt5}{2})^2-\frac{1-\sqrt5}{2})^2]

其实，高中就有这个内容，别不承认，在选修4-1中。我一个高中同学就经常和我提，但我一窍不通。好了，进入正题。

二阶线性递推求通项​

已知数列的前两项 x1,x2x_1,x_2 ，且 已知其二阶线性递推公式 （就是类似斐波那契数列那样），求数列 {xn}\{x_n\} 的通项。

推导​

怎么开始呢？我们可以使用待定系数法构造公比为 bb 的等比数列 {xn+1−axn}\{x_{n+1}-ax_n\}

设：

xn+1−axn=b(xn−axn−1)x_{n+1}-ax_n=b(x_n-ax_{n-1})

移项，合并同类项：

xn+1=(a+b)xn−abxn−1x_{n+1}=(a+b)x_n-abx_{n-1}

根据递推公式可得：

{a+b=pab=−q\left\{\begin{aligned}&a+b=p\\&ab=-q\end{aligned}\right.

好，下面重点来了，根据韦达定理反推解为a,b的方程：

x2−px−q=0x^2-px-q=0

嗯，这就是特征方程，是不是有点像解二阶线性常系数齐次微分方程用到的特征方程？

那么，这个方程接出来之后有什么用呢？

我们根据 aa 和 bb 的关系列出了方程，两个根因该就是 a,ba,b 的值，也就是说，我们可以认为 a,ba,b 是已知的常量。

好现在回到那个我们构造的等比数列，根据等比数列常用的求通项方法：累乘法，可得：

xn+1−axn=bn−1(x2−ax1)(1)x_{n+1}-ax_n=b^{n-1}(x_2-ax_1)_{(1)}

但是，请注意，这里的 aa 和 bb 分别对应特征方程的两个解，可是哪个对应哪个呢？

答案是两种都有可能，咳咳，不信你们直接解关于ab的方程，肯定有两组解

总之， aa 和 bb 对调，还有一个方程：

xn+1−bxn=an−1(x2−bx1)(2)x_{n+1}-bx_n=a^{n-1}(x_2-bx_1)_{(2)}

联立(1)(2)解得：

xn=x2−bx1a−b⋅an−1+x2−ax1b−a⋅bn−1x_n=\frac{x_2-bx_1}{a-b}\cdot a^{n-1}+\frac{x_2-ax_1}{b-a}\cdot b^{n-1}

注意，这里的 x2−bx1a−b\frac{x_2-bx_1}{a-b} 和 x2−ax1b−a\frac{x_2-ax_1}{b-a} 是常数，因此，我们下次使用时不需要这么麻烦的硬解，而是根据这里推出的解的样子再次使用待定系数法

设通项为：

α⋅an−1+β⋅bn−1\alpha\cdot a^{n-1}+\beta\cdot b^{n-1}

代入 n=1,n=2n=1,n=2 ：

{x1=α+βx2=α⋅a+β⋅b\left\{\begin{aligned}&x_1=\alpha+\beta\\&x_2=\alpha\cdot a+\beta\cdot b\end{aligned}\right.

解出 α,β\alpha,\beta ：

{α=x2−bx1a−bβ=x2−ax1b−a\left\{\begin{aligned}&\alpha=\frac{x_2-bx_1}{a-b}\\&\beta=\frac{x_2-ax_1}{b-a}\end{aligned}\right.

总结​

已知数列的前两项 x1,x2x_1,x_2 和递推公式 xn+1=pxn+qxn−1x_{n+1}=px_n+qx_{n-1} ，求数列 {xn}\{x_n\} 的通项。

  1. 解特征方程

    x2−px−q=0x^2-px-q=0

    得出 aa 和 bb

  2. 设通项为 xn=α⋅an−1+β⋅bn−1x_n=\alpha\cdot a^{n-1}+\beta\cdot b^{n-1} 并代入 n=1,n=2n=1,n=2 解出 α,β\alpha,\beta ：

    {x1=α+βx2=α⋅a+β⋅b\left\{\begin{aligned}&x_1=\alpha+\beta\\&x_2=\alpha\cdot a+\beta\cdot b\end{aligned}\right. {α=x2−bx1a−bβ=x2−ax1b−a\left\{\begin{aligned}&\alpha=\frac{x_2-bx_1}{a-b}\\&\beta=\frac{x_2-ax_1}{b-a}\end{aligned}\right.

  3. 写出通项。

例子：斐波那契数列​

已知数列的前两项 x1=1,x2=1x_1=1,x_2=1 和递推公式 xn+1=xn+xn−1x_{n+1}=x_n+x_{n-1} ，求数列 {xn}\{x_n\} 的通项。

解特征方程：

r2−r−1=0r^2-r-1=0 r1=1+52,r1=1−52r_1=\frac{1+\sqrt{5}}{2},r_1=\frac{1-\sqrt{5}}{2}

设通项为：

xn=α⋅(1+52)n−1+β⋅(1+52)n−1x_n=\alpha\cdot(\frac{1+\sqrt{5}}{2})^{n-1}+\beta\cdot(\frac{1+\sqrt{5}}{2})^{n-1}

代入 x1=1,x2=1x_1=1,x_2=1 ：

{α+β=11+52⋅α+1−52⋅β=1\left\{\begin{array}{} \alpha+\beta=1\\ \frac{1+\sqrt5}{2}\cdot\alpha+\frac{1-\sqrt5}{2}\cdot\beta=1 \end{array}\right.

解得：

{α=5+510β=5−510\left\{\begin{array}{} \alpha=\frac{\sqrt5+5}{10}\\ \beta=\frac{\sqrt5-5}{10} \end{array}\right.

因此：

xn=15[(1+52)2−1−52)2]x_n=\frac{1}{\sqrt5}[(\frac{1+\sqrt5}{2})^2-\frac{1-\sqrt5}{2})^2]

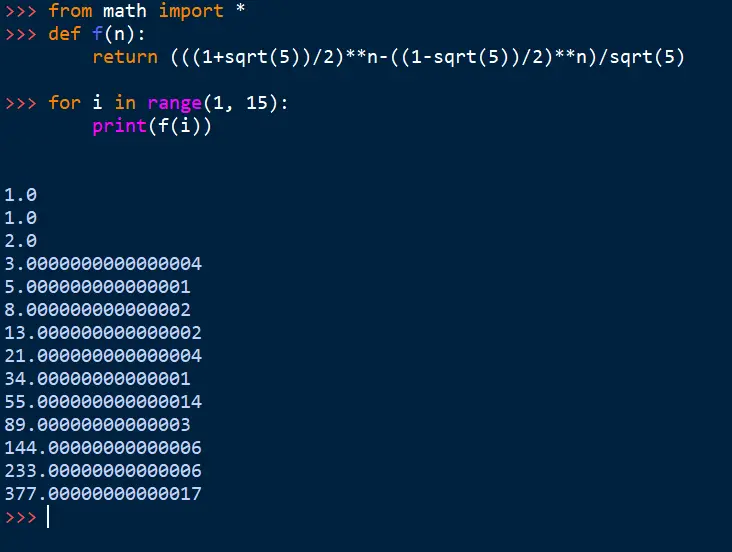
这个公式非常神奇，虽然看起来令人头皮发麻，但算出来居然每一项都是整数！

from math import *

def f(n):
    return (((1+sqrt(5))/2)**n-((1-sqrt(5))/2)**n)/sqrt(5)

for i in range(1, 15):
    print(f(i))

python运行结果